선형회귀(linear regression)
선형회귀(linear regression) 회귀란? 관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한뒤 적합도를 측정해 내는 분석 방법 선형회귀 가장 기본적이고 널리 사용되는 기계 학습 알고리즘 중
ursobad.tistory.com
로지스틱 회귀(Logistic Regression)
종속 변수와 독립 변수 간의 관계를 구체적으로 나타낸다.
선형 회귀처럼 연속된 값을 예측하는 것이 아니라 종속변수가 범주형 데이터일 때 사용한다.
회귀를 사용하여 범주에 속할 확률을 예측한다.
- 가능성이 더 높은 범주로 분류하는 알고리즘이다.
# 독립 변수 : 독립 변수는 입력값이나 원인
# 종속 변수 : 종속 변수는 결과물이나 효과
# 범주형 데이터 : 0 또는 1처럼 이진으로 나타나 있는 데이터
# 이항 로지스틱 회귀 : 종속 변수가 2개인 binary 형태일 때 EX) 날씨(hot, cold)
# 다항 로지스틱 회귀 : 종속 변수가 3개 이상 multi 형태일 때 EX) 날씨(rainy, sunny, cloudly)
이진 분류
공부한 시간에 따라서 시험 합격률이 달라진다고 했을때 선형 회귀로 데이터를 가장 잘 나타내는 직선을 그려보면 아래와 같다.

직선으로 그려졌기때문에 2시간 이상 공부하지 않으면 합격 확률이 음수가 된다. 이건 말이 안 된다.
위 문제점을 해결하기 위해서 이진 분류 문제를 풀 때는 로지스틱 회귀를 사용한다.
로지스틱 회귀로 다시 그려보면 아래와 같은 선을 그릴 수 있다.
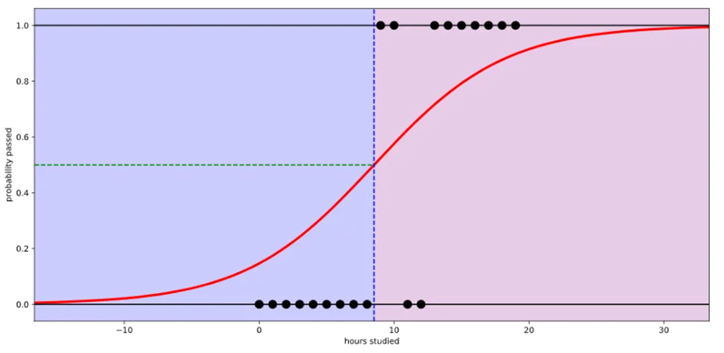
이제는 0부터 1까지의 범위 안에서 값이 나온다.
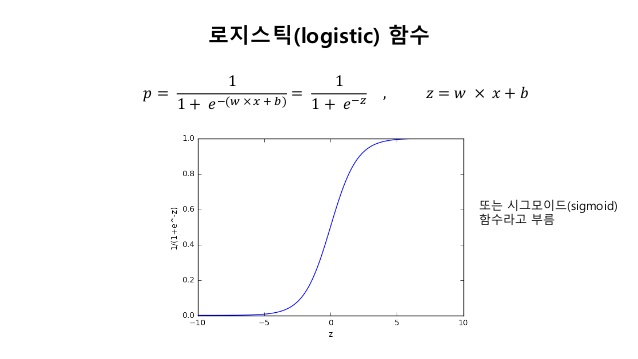
시그모이드 함수(로지스틱 함수)

위와 같은 형태를 지닌 함수를 시그모이드 함수라고 한다.
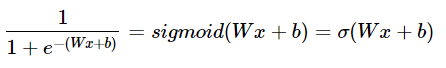
σ로 축약해서 표현하기도 한다.
시그모이드 함수는 입력값이 커지면 1에 수렴하고, 입력값이 작아지면 0에 수렴한다. 0부터의 1까지의 값을 가지는데 출력 값이 0.5 이상이면 1(True), 0.5이하면 0(False)으로 만들면 이진 분류 문제로 사용할 수 있다.
Odds(승산)
어떤 사건이 일어날 확률을 그 사건이 일어나지 않을 확률로 나눈 것
사건이 일어날 확률 p분의 사건이 일어나지 않을 확률 1-p
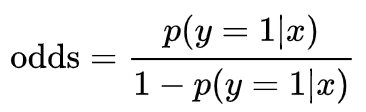
예를 들어서 게임에서 이길 확률이 1/5, 질 확률이 4/5이면 게임에서 이길 odds는 1/4가 된다.
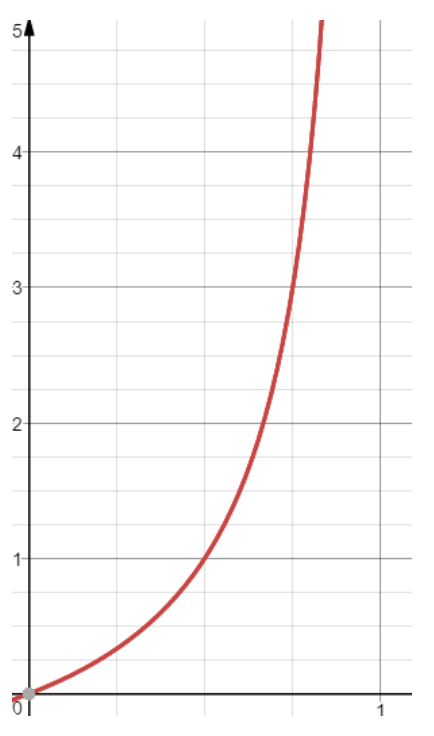
p가 1에 가까울수록 값이 커지고 p가 0이면 0이 된다.
0 < odds < ∞의 범위에 속하고 비대칭성을 가진다는 것을 알 수 있다
로짓(Logit), 로그 오즈(Log odds)
모든 실수를 범위로 해야 하기 때문에 odds에 로그함수를 취해준다.
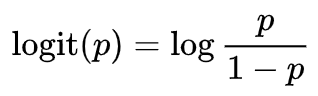
log(odds)의 범위는 이제 아래와 같이 형성되고 대칭성 또한 가지게 된다.
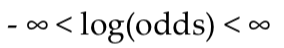
위 과정을 정리하면 아래와 같다.
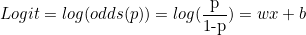
로짓 변환을 마치면 입력 0~1 사이에 대해 출력 값의 범위는( –∞,∞)가 되고, 0 <= P <=1을 만족한다.
복잡했던 로지스틱 함수가 wx+b의 선형 결합의 형태로 바뀐다.
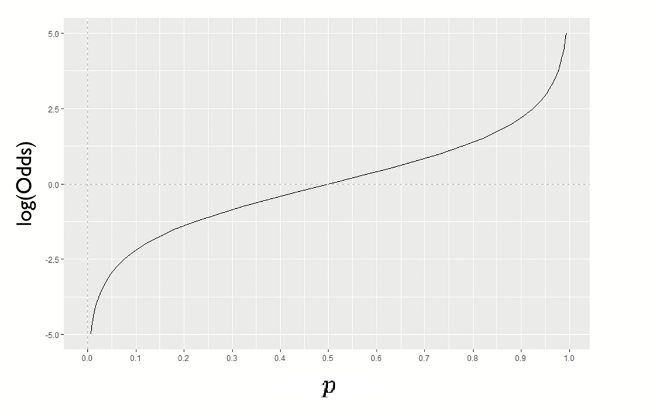
이런 로짓 함수에 역함수를 취하면 시그모이드 함수(로지스틱 함수)가 된다.
로지스틱 손실 함수(cross-entropy)
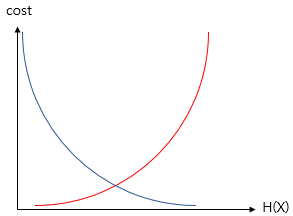
로지스틱 회귀에서도 경사 하강법을 사용하지만 비용 함수로는 평균제곱 오차를 사용하지 않는다. 시그모이드 함수에 평균제곱 오차를 비용함수로 하여 그래프를 그리면 아래와 같이 나오기 때문이다.

선형 회귀에서의 목적이 평균 제곱 오차를 줄이는 것이었다면 로지스틱 회귀에서는 로그손실(log loss)를 줄이는것이 목적이다.
이때 로그 손실을 두 가지로 나누어서 이해해야 하는데 그 이유는 결국엔 1이냐 0이냐의 이진 분류이기 때문이다.
만약 y의 실제값이 0일 때 y값이 1에 가까워지면 오차가 커지며 y의 실제값이 1일 때 y값이 0에 가까워지면 오차가 커짐을 의미한다. 이를 로그함수를 통해 표현할 수 있다.
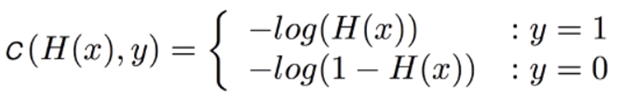
# y : 타깃 값
# H(x) : 활성화 함수의 출력 값(1~0 사이의 값)
결론적으로 로지스틱 회귀의 비용 함수를 아래와 같이 정리된다.
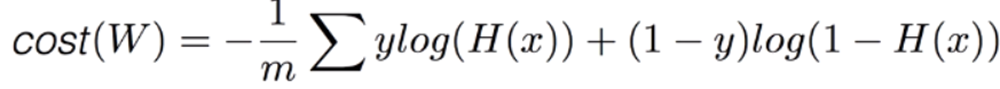
비용 함수에 선형 회귀와 같이 경사 하강법을 사용하여 로그 손실을 최소화하는 계수를 찾는다.
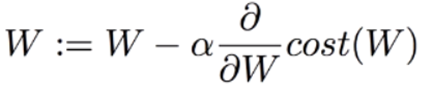
임계값(Classification Threshold)
분류를 하기 위해 기준이 되는 값
기본 임계값은 보통 0.5이지만 필요에 따라 모델의 임계값은 변경할 수 있음
암을 진단하는 로지스틱 회귀 모델을 작성하는 경우에는 혹시 모를 경우에 대비하여 좀 더 민감하게 확인하기 위해 0.3이나 0.4로 임계값을 낮춰 모델의 민감도를 높일 필요가 있다.
#빨간 그래프 : 암이 걸리지 않은 사람
#노란 그래프 : 암 환자
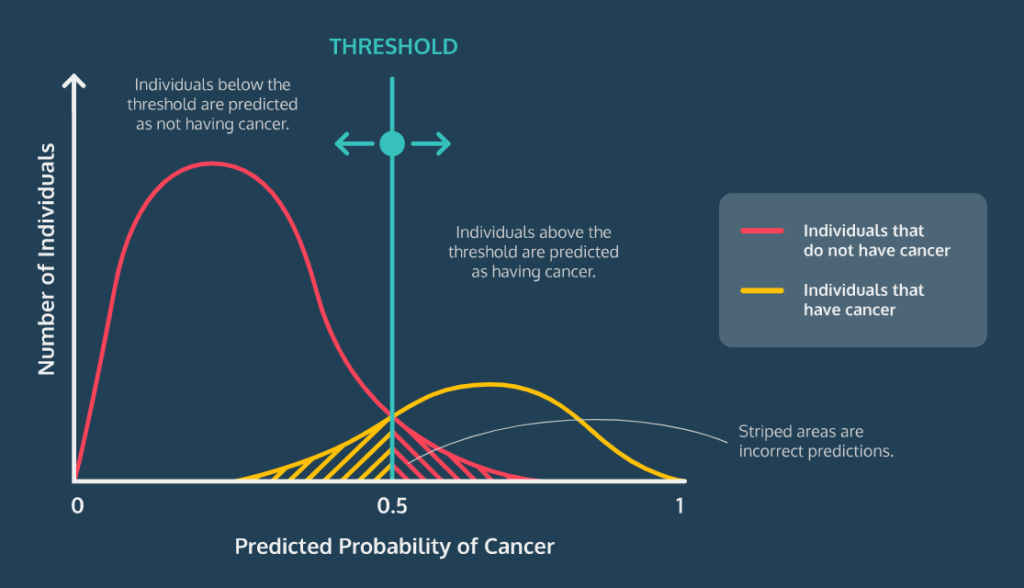
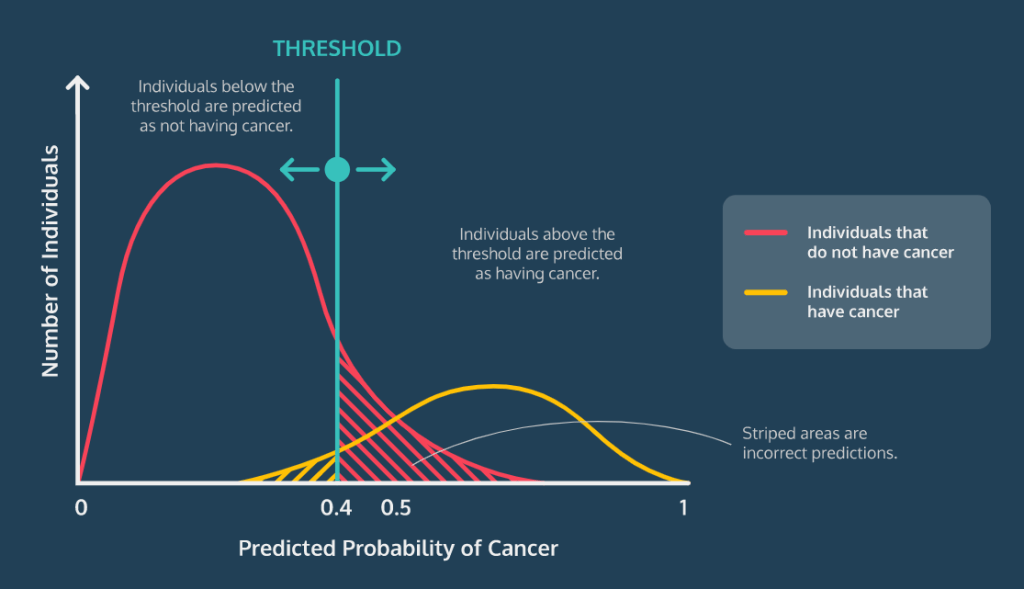
임계값이 0.4일 때 0.5일 때보다 더 잘 분류한다는 것을 알 수 있다.
구현(sklearn)
1. numpy, matplotlib, sklearn을 불러온다.
from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt
2. 임의의 데이터 셋을 만든다.
x = []
y = []
#[0,0] ~ [99,99]까지의 데이터 생성
for i in range(100):
for j in range(100):
x.append([i, j])
x = np.array(x) #넘파이 배열로 바꿈
np.random.shuffle(x) #순서를 섞는다
for i in range(10000):
if x[i, 0] * 2 + x[i, 1] > 150: #x[0] * 2 +x[1]이 150 이상이면 y값이 1
y.append(1)
else:
y.append(0)
y = np.array(y)
3. 모델을 만들고 fit()을 통해 학습시킨다.
model = LogisticRegression().fit(x, y)
4. 시각화한다.
test_x = x[:30]
test_y = model.predict(test_x)
for i in range(30):
if test_y[i] == 0:
plt.scatter(test_x[i:i+1, 0], test_x[i:i+1, 1], c='red')
else:
plt.scatter(test_x[i:i+1, 0], test_x[i:i+1, 1], c='blue')
print(model.coef_, model.intercept_) #coef_ : 추정된 가중치 벡터(w), intercept_ : 추정된 상수항(b)
x1, y1 = [-model.intercept_ / model.coef_[0][0],
(-model.intercept_ -model.coef_[0][1]*100) / model.coef_[0][0]], [0, 100]
plt.plot(x1, y1, color='black')
plt.show()
--출력--
[[5.35418259 2.67754192]] [-402.92454625]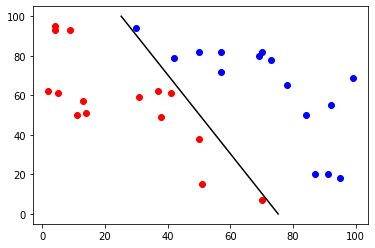
예제 코드
'Emotion > 인공지능 기초' 카테고리의 다른 글
| Opencv 얼굴 인식(사진) (0) | 2020.11.27 |
|---|---|
| 앙상블 학습법(Ensemble Learning) (0) | 2020.09.29 |
| SVM(Support Vector Machine) 알고리즘 (0) | 2020.09.24 |
| 선형회귀(linear regression) (0) | 2020.09.24 |
| 나이브 베이즈 (0) | 2020.09.24 |
