선형회귀(linear regression)
회귀란?
관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한뒤 적합도를 측정해 내는 분석 방법
선형회귀
가장 기본적이고 널리 사용되는 기계 학습 알고리즘 중 하나
독립 변수 x를 사용해 종속 변수 y의 움직임을 예측하고 설명한다
간단하게 일차함수의 개념 y = ax + b의 직선을 임의로 그려놓고, 그 직선을 바탕으로 예측하는 것
#독립 변수 : 독립 변수는 입력값이나 원인
#종속 변수 : 종속 변수는 결과물이나 효과
단순 선형회귀(simple linear regression) : 하나의 x 값만으로도 y 값을 설명할 수 있는 것
다중 선형회귀(multiple linear regression) : x 값이 여러 개 필요로 할 때 사용
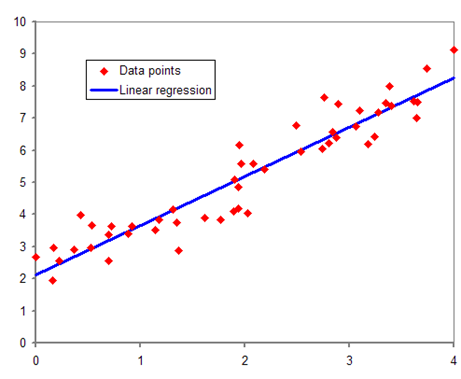
Error(에러)
사용자가 예측하기 위해 만든 모델 y = ax + b 직선과 실제 데이터 사이의 y값 차이
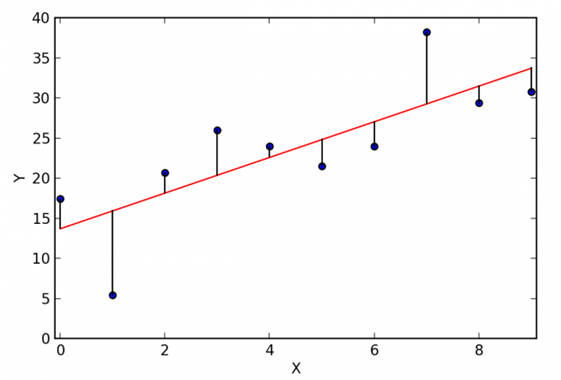
square error
실제 데이터 y값과 예측 모델 y값 차이를 제곱한 값
error를 제곱하는 이유
1. 값이 더 커지기 때문에 에러가 조금이라도 있다면 값이 증폭되어 큰값과 작은 값의 비교가 쉽다
2. 알고리즘에서 필요한 편미분 계산이 용이하다.
mean square error(평균 제곱 오차)
square error를 평균 낸 값
mean square error(평균 제곱 오차)의 수학적 표현
아래같은 그래프가 있다고 가정해보자.
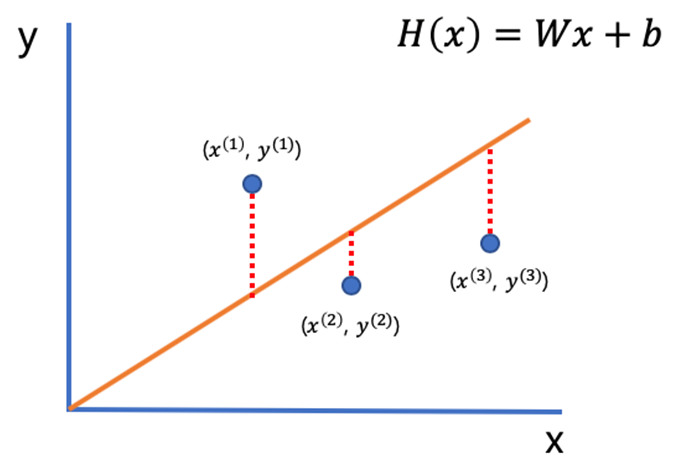
위 그래프의 평균 제곱 오차(MSE)를 계산해보면 예측값 H(x)에서 실제값 y를 뺀 후 제곱하여 데이터의 수인 3으로 나눈다.
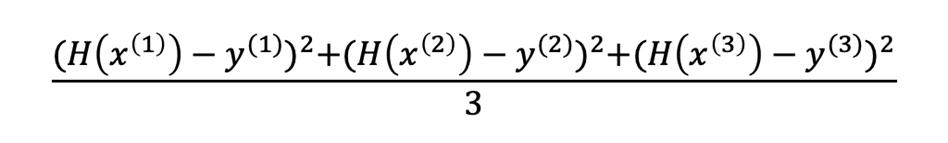
일반화 하면 이렇게 된다.
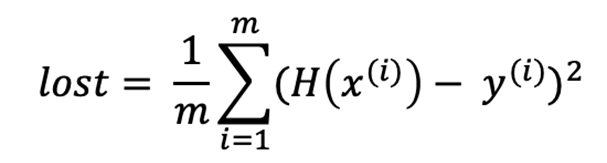
Gradient Descent 알고리즘(경사 하강법)
가장 best한 선형회귀 모델을 만들기 위하여 사용되는 알고리즘
비용함수(Cost function) : mean square error(평균 제곱 오차)와 같다
최소 평균 제곱 오차(Least Mean Square Error) : 비용함수 즉, 평균제곱오차를 최소로 만드는 것
목적함수(objective function) : Cost function을 최저로 만드는 목적을 가진 함수
Gradient Descent 알고리즘(경사 하강법)의 수학적 표현
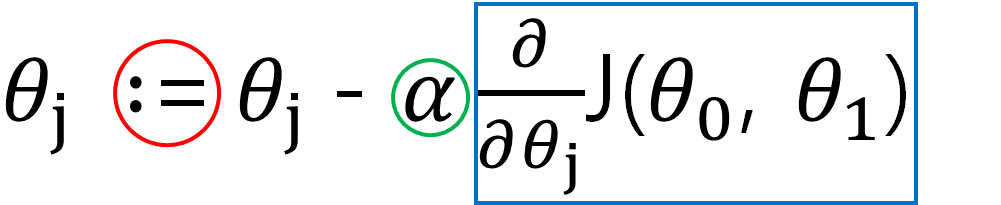
∶= (빨간 원) - 대입 연산자. C언어의 ==과 같이 우변에 있는 것을 좌변에 대입한다.
α (알파, 초록 원) - 학습률(Learning rate), 2차함수 그래프에서 경사를 타고 내려갈 정도를 정한다.
미분계수(파란 박스) - 비용함수(MSE)를 알파에 대해 미분한 함수, 한 점에서의 기울기 값
사용자의 최종 목적은 아래 비용함수 그래프에서 MSE를 최소로 만드는 것이다.
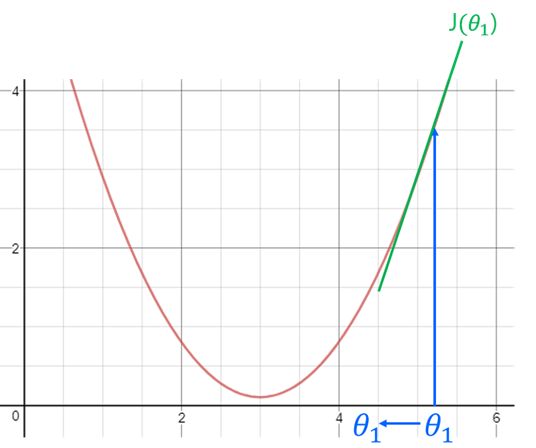
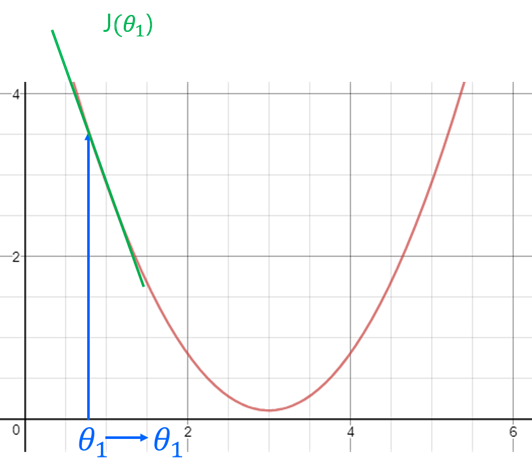
먼저 미분계수를 통하여 한 점의 기울기값을 구한다. 기울기 값이 양수라면 0에 가까워지기 위해서는 현재의 기울기에서 +값을 빼서 0에 가깝게 만든다. 또 기울기의 값이 음수라면 -값을 빼서 0에 가깝게 만들 수 있다.
학습률(Learning rate)
학습률이 너무 낮을때
경사를 타고 내려오는데 시간이 너무 오래 걸려 최솟값을 찾는데 많은 연산과 시간이 걸린다.
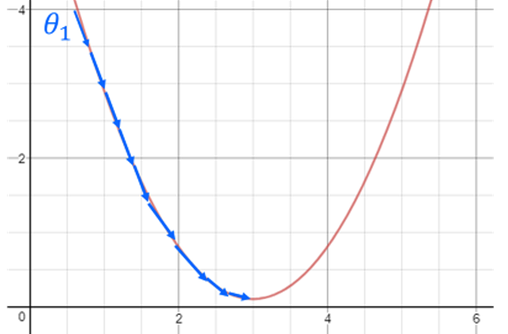
학습률이 너무 높을때
최솟값에 대하여 점점 멀어질 수 있다.
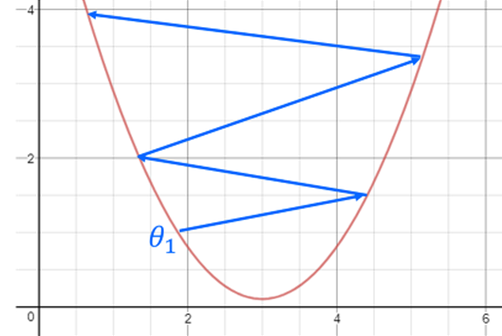
구현(numpy)
1. numpy와 matplotlib를 불러온다.
import numpy as np
import matplotlib.pyplot as plt
2. y = 0.2 * x + 0.5 관계를 가지는 데이터를 생성한다. np.random.normal 함수를 통해 약간의 변동값을 주었다.
x_data = np.array([])
y_data = np.array([])
for i in range(1000):
x1= np.random.normal(0.0, 0.55)
y1 = x1*0.2+0.5 + np.random.normal(0.0, 0.05)
x_data = np.append(x_data, x1)
y_data = np.append(y_data, y1)
3. W와 b를 0으로 초기화하고 데이터에 대해 산점도를 출력해본다.
W = 0.0
b = 0.0
n_data = len(x_data) #1000
plt.scatter(x_data,y_data) #x,y산점도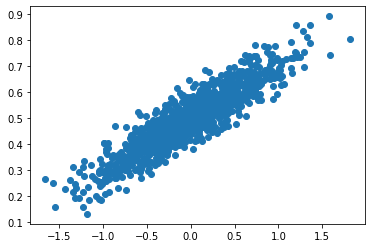
4. 학습률(Learning rate)과 반복할 횟수를 설정한다.
epochs = 5000
learning_rate = 0.01
5. 비용함수와 경사하강법을 이용하여 구현한다.
for i in range(epochs): #5000번 반복한다
hypothesis = x_data * W + b #y = w * x + b
cost = np.sum((hypothesis - y_data) ** 2) / n_data #mse 계신
gradient_w = np.sum((W * x_data - y_data + b) * 2 * x_data) / n_data #목적 함수인 W에대하여 편미분
gradient_b = np.sum((W * x_data - y_data + b) * 2) / n_data #b에 대하여 편미분
#W, b 업데이트
W -= learning_rate * gradient_w
b -= learning_rate * gradient_b
if i%100 == 0: #100번째마다 그래프 출력
y_hat = x_data * W + b
print('W: {:10f}'.format(W))
print('b: {:10f}'.format(b))
plt.scatter(x_data,y_data) #x,y산점도
plt.plot(x_data, y_hat, color='red')
plt.legend()
plt.show()hypothesis에 W*x+b를 넣는다.
cost변수 안에 비용함수(MSE)를 넣는다.
gradient_w와 gradient_b에는 각각 W와 b를 편미분한 값을 넣고 W,b에서 빼서 업데이트 한다.
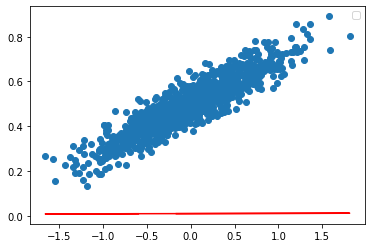
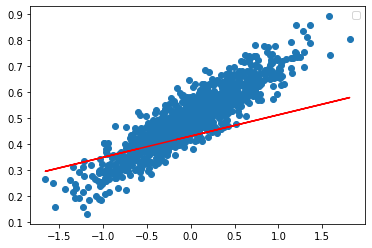
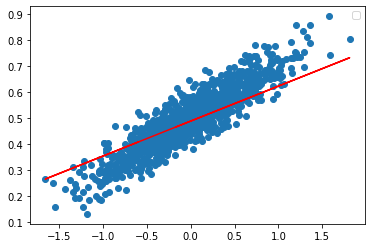
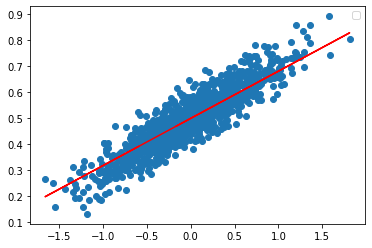
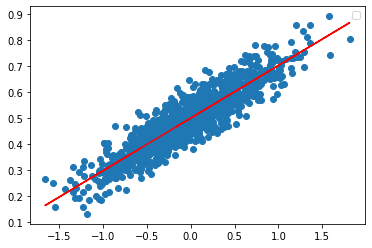
이후 그래프는 변화가 없다.
6. 선형회귀를 통해 예측한 W와, b값을 출력해본다.
print('W: {:10f}'.format(W))
print('b: {:10f}'.format(b))
--출력--
W: 0.202191
b: 0.500400W와 b가 설정했던 0.2와 0.5에 가깝게 출력되는 것을 볼 수 있다.
구현(tensorflow)
1. tensorflow, numpy, matplotlib를 불러온다.
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
2. y = 0.2 * x + 0.5 관계를 가지는 데이터를 생성한다. np.random.normal 함수를 통해 약간의 변동값을 주었다.
x_data = np.array([])
y_data = np.array([])
for i in range(1000):
x1= np.random.normal(0.0, 0.55)
y1 = x1*0.2+0.5 + np.random.normal(0.0, 0.03)
x_data = np.append(x_data, x1)
y_data = np.append(y_data, y1)
plt.scatter(x_data,y_data) #x,y산점도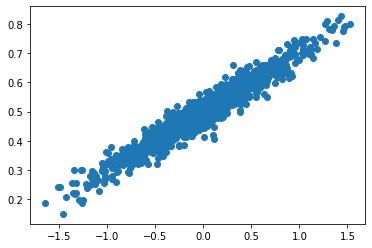
3. 모델 구축
model = tf.keras.Sequential() #모델 구축
model.add(tf.keras.layers.Dense(1, input_shape=(1,))) #입력데이터(x_data)가 1개이므로 input_shape가 1
4. 모델 컴파일
학습 알고리즘은 경사하강법을 사용하고 손실함수는 MSE를 사용한다.
총 학습해야할 파라미터는 W,b로 2개이다.
model.compile(loss = 'mse', optimizer = tf.keras.optimizers.SGD(learning_rate=0.01))
model.summary() #모델 구조 확인
--출력--
Model: "sequential_6"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_6 (Dense) (None, 1) 2
=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
5. 학습
.fit()을 이용하여 학습한다.
model.fit(x_data,y_data,epochs=1000)
6. 학습후의 W와 b를 출력해 본다,
model.weights
--출력--
[<tf.Variable 'dense_6/kernel:0' shape=(1, 1) dtype=float32, numpy=array([[0.2006424]], dtype=float32)>,
<tf.Variable 'dense_6/bias:0' shape=(1,) dtype=float32, numpy=array([0.50038403], dtype=float32)>]W가 0.2006, b가 0.5003으로 거의 근접한것을 볼 수 있다.
plt.scatter(x_data,y_data) #x,y산점도
plt.plot(x_data, model.predict(x_data), color="r")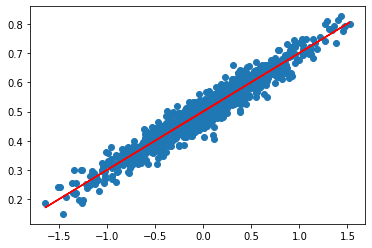
예제 코드
## 아직 텐서플로우 사용방법을 잘 모르겠다
'Emotion > 인공지능 기초' 카테고리의 다른 글
| 로지스틱 회귀(Logistic Regression) (0) | 2020.09.29 |
|---|---|
| SVM(Support Vector Machine) 알고리즘 (0) | 2020.09.24 |
| 나이브 베이즈 (0) | 2020.09.24 |
| 랜덤 포레스트 (0) | 2020.09.16 |
| 의사결정 트리 CART (0) | 2020.09.16 |
